Уравнение плоскости. Как составить уравнение плоскости?
Взаимное расположение плоскостей. Задачи

Пространственная геометрия не намного сложнее «плоской» геометрии, и наши полёты в пространстве начинаются с данной статьи. Для усвоения темы необходимо хорошо разобраться в векторах , кроме того, желательно быть знакомым с геометрией плоскости – будет много похожего, много аналогий, поэтому информация переварится значительно лучше. В серии моих уроков 2D-мир открывается статьёй Уравнение прямой на плоскости . Но сейчас Бэтмен сошёл с плоского экрана телевизора и стартует с космодрома Байконур.

Начнём с чертежей и обозначений. Схематически плоскость можно нарисовать в виде параллелограмма, что создаёт впечатление пространства:

Плоскость бесконечна, но у нас есть возможность изобразить лишь её кусочек. На практике помимо параллелограмма также прорисовывают овал или даже облачко. Мне по техническим причинам удобнее изображать плоскость именно так и именно в таком положении. Реальные плоскости, которые мы рассмотрим в практических примерах, могут располагаться как угодно – мысленно возьмите чертёж в руки и покрутите его в пространстве, придав плоскости любой наклон, любой угол.

Обозначения : плоскости принято обозначать маленькими греческими буквами , видимо, чтобы не путать их с прямой на плоскости или с прямой в пространстве . Я привык использовать букву . На чертеже именно буква «сигма», а вовсе не дырочка. Хотя, дырявая плоскость, это, безусловно, весьма забавно.

В ряде случаев для обозначения плоскостей удобно использовать те же греческие буквы с нижними подстрочными индексами, например, .

Очевидно, что плоскость однозначно определяется тремя различными точками, не лежащими на одной прямой. Поэтому достаточно популярны трёхбуквенные обозначения плоскостей – по принадлежащим им точкам, например, и т.д. Нередко буквы заключают в круглые скобки: , чтобы не перепутать плоскость с другой геометрической фигурой.

Для опытных читателей приведу меню быстрого доступа :

• Как составить уравнение плоскости по точке и двум векторам?
• Как составить уравнение плоскости по точке и вектору нормали?

и мы не будем томиться долгими ожиданиями:

Общее уравнение плоскости

Общее уравнение плоскости имеет вид , где коэффициенты одновременно не равны нулю.

Ряд теоретических выкладок и практических задач справедливы как для привычного ортонормированного базиса, так и для аффинного базиса пространства (если масло - масляное, вернитесь к уроку Линейная (не) зависимость векторов. Базис векторов ). Для простоты будем полагать, что все события происходят в ортонормированном базисе и декартовой прямоугольной системе координат.

А теперь немного потренируем пространственное воображение. Ничего страшного, если у вас оно плохое, сейчас немного разовьём. Даже для игры на нервах нужны тренировки.

В самом общем случае, когда числа не равны нулю, плоскость пересекает все три координатные оси. Например, так:

Ещё раз повторю, что плоскость бесконечно продолжается во все стороны, и у нас есть возможность изобразить только её часть.

Рассмотрим простейшие уравнения плоскостей:

Как понимать данное уравнение? Вдумайтесь: «зет» ВСЕГДА, при любых значениях «икс» и «игрек» равно нулю. Это уравнение «родной» координатной плоскости . Действительно, формально уравнение можно переписать так: , откуда хорошо видно, что нам по барабану, какие значения принимают «икс» и «игрек», важно, что «зет» равно нулю.

Аналогично:
– уравнение координатной плоскости ;
– уравнение координатной плоскости .

Немного усложним задачу, рассмотрим плоскость (здесь и далее в параграфе предполагаем, что числовые коэффициенты не равны нулю). Перепишем уравнение в виде: . Как его понимать? «Икс» ВСЕГДА, при любых значениях «игрек» и «зет» равно некоторому числу . Эта плоскость параллельна координатной плоскости . Например, плоскость параллельна плоскости и проходит через точку .

Аналогично:
– уравнение плоскости, которая параллельна координатной плоскости ;
– уравнение плоскости, которая параллельна координатной плоскости .

Добавим членов: . Уравнение можно переписать так: , то есть «зет» может быть любым. Что это значит? «Икс» и «игрек» связаны соотношением , которое прочерчивает в плоскости некоторую прямую (узнаёте уравнение прямой на плоскости ?). Поскольку «зет» может быть любым, то эта прямая «тиражируется» на любой высоте. Таким образом, уравнение определяет плоскость, параллельную координатной оси

Аналогично:
– уравнение плоскости, которая параллельна координатной оси ;
– уравнение плоскости, которая параллельна координатной оси .

Если свободные члены нулевые, то плоскости будут непосредственно проходить через соответствующие оси. Например, классическая «прямая пропорциональность»: . Начертите в плоскости прямую и мысленно размножьте её вверх и вниз (так как «зет» любое). Вывод: плоскость, заданная уравнением , проходит через координатную ось .

Завершаем обзор: уравнение плоскости проходит через начало координат. Ну, здесь совершенно очевидно, что точка удовлетворяет данному уравнению.

И, наконец, случай, который изображён на чертеже: – плоскость дружит со всеми координатными осями, при этом она всегда «отсекает» треугольник, который может располагаться в любом из восьми октантов.

Линейные неравенства в пространстве

Для понимания информации необходимо хорошо изучить линейные неравенства на плоскости , поскольку многие вещи буду похожи. Параграф будет носить краткий обзорный характер с несколькими примерами, так как материал на практике встречается довольно редко.

Если уравнение задаёт плоскость, то неравенства
задают полупространства . Если неравенство нестрогое (два последних в списке), то в решение неравенства кроме полупространства входит и сама плоскость.

Пример 5

Найти единичный нормальный вектор плоскости .

Решение : Единичный вектор – это вектор, длина которого равна единице. Обозначим данный вектор через . Совершенно понятно, что векторы коллинеарны:

Сначала из уравнения плоскости снимем вектор нормали: .

Как найти единичный вектор? Для того чтобы найти единичный вектор , нужно каждую координату вектора разделить на длину вектора .

Перепишем вектор нормали в виде и найдём его длину:

Согласно вышесказанному:

Ответ :

Проверка: , что и требовалось проверить.

Читатели, которые внимательно изучили последний параграф урока , наверное, заметили, что координаты единичного вектора – это в точности направляющие косинусы вектора :

Отвлечёмся от разобранной задачи: когда вам дан произвольный ненулевой вектор , и по условию требуется найти его направляющие косинусы (см. последние задачи урока Скалярное произведение векторов ), то вы, по сути, находите и единичный вектор, коллинеарный данному. Фактически два задания в одном флаконе.

Необходимость найти единичный вектор нормали возникает в некоторых задачах математического анализа.

С выуживанием нормального вектора разобрались, теперь ответим на противоположный вопрос:

Как составить уравнение плоскости по точке и вектору нормали?

Эту жёсткую конструкцию вектора нормали и точки хорошо знает мишень для игры в дартс. Пожалуйста, вытяните руку вперёд и мысленно выберите произвольную точку пространства, например, маленькую кошечку в серванте. Очевидно, что через данную точку можно провести единственную плоскость, перпендикулярную вашей руке.

Уравнение плоскости, проходящей через точку перпендикулярно вектору , выражается формулой:

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1 и α 2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.

Условие параллельности двух плоскостей.

Две плоскости α 1 и α 2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

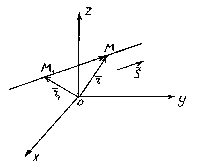
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

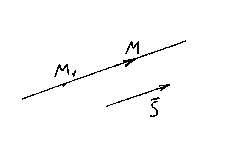
Пусть М 1 (x 1 , y 1 , z 1) – точка, лежащая на прямой l , и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t . Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t , y = –1 + 2t , z = 1 –t .

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t , получим уравнения прямой в виде

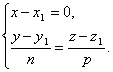
Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .

Примеры.

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:

Решив эту систему, найдем точку M 1 (1;2;0).

Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.

Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

.

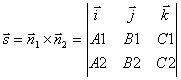Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l : .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн .

Пусть задана произвольная декартова прямоугольная система координат Oxyz . Общим уравнением плоскости называется линейное уравнение вида:

Ax+By+Cz+D =0,

(1)

где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля.

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α . Выберем оси Ox и Oy так, чтобы они располагались на плоскости α , а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z= 0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z= 0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Пусть фиксирована произвольная декартова прямоугольная система координат Oxyz . Рассмотрим линейное уравнение (1), где хотя бы один из элементов A , B и C отлично от нуля. Тогда уравнение (1) имеет хотя бы одно решение x 0 , y 0 , z 0 . Действительно. Пусть из коэффициентов A ≠0. Возьмем произвольные числа y 0 , z 0 . Тогда

Вычитая из уравнения (1) тождество (2), получим

Покажем, что (3) определяет некоторую плоскость, проходящую через точку M 0 (x 0 , y 0 , z 0) и перпендикулярную вектору n ={A ,B ,C } (n ≠0, так как хотя бы один из чисел A ,B ,C отлично от нуля).

Если точка M 0 (x 0 , y 0 , z 0) принадлежит плоскости α , то ее координаты удовлетворяют уравнению (3), т.к. векторы n ={A ,B ,C } и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

.

Если же точка M (x , y , z ) не лежит на плоскости α , то векторы n ={A ,B ,C } и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M (x , y , z ) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C ) перпендикулярен плоскости Ax +By +Cz +D =0.

Вектор n =(A,B,C ) называется нормальным вектором плоскости , определяемой линейным уравнением (1).

Утверждение 2. Если два общих уравнения плоскости

Доказательство. Так как уравнения (4) и (5) определяют одну и ту же плоскость, то нормальные векторы n 1 ={A 1 ,B 1 ,С 1 } и n 2 ={A 2 ,B 2 , С 2 } коллинеарны. Так как векторы n 1 ≠0, n 2 ≠0, то существует такое число λ , что n 2 =n 1 λ . Отсюда имеем: A 2 =A 1 λ , B 2 =B 1 λ , С 2 =С 1 λ . Докажем, что D 2 =D 1 λ . Очевидно, что совпадающие плоскости имеют общую точку M 0 (x 0 , y 0 , z 0), так что

Так как выполнены первые три равенства из выражений (6), то D 1 λ −D 2 =0. Т.е. D 2 =D 1 λ . Утверждение доказано.

Неполные уравнения плоскости

Определение 1. Общее уравнение плоскости (1) называется полным , если все коэффициенты A, B, C, D отличны от нуля. Если же хотя бы один из коэффициентов A, B, C, D равен нулю, то общее уравнение плоскости называется неполным .

Рассмотрим все возможные варианты неполных уравнений плоскости:

При D A x +B y +C z =0, проходящей через начало координат (Рис.2). Действительно, точка O (0,0,0) удовлетворяет этой системы линейных уравнений.

При A =0, имеем уравнение плоскости B y +C z +D =0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n ={0,B ,C } лежит на координатной плоскости Oyz .

При B =0, имеем уравнение плоскости A x +C z +D =0, которая параллельна оси Oy (Рис.4).

При C =0, имеем уравнение плоскости A x +B y +D =0, которая параллельна оси Oz (Рис.5).

При A =0,B =0 имеем уравнение плоскости C z +D Oxy (Рис.6).

При B =0,C =0 имеем уравнение плоскости A x +D =0, которая параллельна координатной плоскости Oyz (Рис.7).

При A =0,C =0 имеем уравнение плоскости B y +D =0, которая параллельна координатной плоскости Oxz (Рис.8).

При A =0,B =0,D =0 имеем уравнение плоскости C z Oxy (Рис.9).

При B =0,C =0,D =0 имеем уравнение плоскости A x =0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A =0,C =0,D =0 имеем уравнение плоскости B y =0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M (4,−1,2) параллельной координатной плоскости Oxy .

Решение. Общее уравнение плоскости, проходящей через некоторую точку M (x 0 ,y 0 ,z 0) имеет вид (3). Подставляя координаты точки M в (3), получим:

z −2=0

Ответ: +3y +z =0.

Ответ:

2x +3y +z =0.

Онлайн калькулятор для построения общего уравнения плоскости находится . Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Можно показать, что любое уравнение первой степени относительно декартовых координат x, y, z представляет собой уравнение некоторой плоскости. Это уравнение записывается в виде:

Ax+By+Cz+D =0

и называется общим уравнением плоскости, причём координаты A, B, C здесь являются координатами нормального вектора плоскости.

Рассмотрим частные случаи общего уравнения. Выясним, как располагается плоскость относительно системы координат, если один или несколько коэффициентов уравнения обращаются в ноль.

1. Свободный член равен нулю D = 0.

В этом случае уравнение плоскости принимает видAx+Cy+Bz =0. Т.к. числа x =0, y =0, z =0 удовлетворяют уравнению плоскости, то она проходит через начало координат. Аналогично, если B = 0, то плоскость параллельна оси Oy и C = 0 – плоскость параллельна оси Oz . Т.о., если в уравнении плоскости один из коэффициентов при текущей координате равен нулю, то плоскость параллельна соответствующей координатной оси.

1. Коэффициент при текущей координате и свободный член равны нулю. Например, A = D = 0. В этом случае уравнению By + Cz = 0 соответствует плоскость, проходящая через начало координат (согласно п.1). Кроме того, учитывая п.2, данная плоскость должна быть параллельна оси Ox . Следовательно, плоскость проходит через ось Ox .

Аналогично, при B=D =0 плоскость Ax+Cz =0 проходит через ось Oy . При C=D =0 плоскость проходит через ось Oz .

1. Два коэффициента при текущих координатах раны нулю. Пусть, например, A=B =0. Тогда плоскость Cz+D =0 в силу п.2 будет параллельна осям Ox и Oy , а следовательно параллельна координатной плоскости xOy , и проходит через точку с координатой. Аналогично, уравнениям Ax+D =0 и By+D =0 соответствуют плоскости, параллельные координатным плоскостям yOz и xOz .
2. Два коэффициента при текущих координатах и свободный член равны нулю. Пусть, например, A=B=D =0. Тогда уравнение плоскости имеет вид Cz =0 или z =0. Эта плоскость проходит через начало координат и параллельна осям Ox и Oy , т. е. уравнение определяет координатнуюплоскость xOy . Аналогично, x =0 – уравнение координатной плоскости yOz и y =0 – плоскость xOz .

Примеры.

1. Составить уравнение плоскости, проходящей параллельно оси Oy , через точки M 1 (1; 0; -1), M 2 (-1; 2;0).

Так как ось Oy параллельна , то уравнение плоскости Ax+Cy+D =0. Учитывая, что M 1 Î α, M 2 Î α, подставим координаты этих точек в уравнение и получим систему из двух линейных уравнений с тремя неизвестными

Положив D = 1, найдем A = 1 и C = 2. Следовательно, уравнение плоскости имеет видx+ 2z +1=0.

1. Составить уравнение плоскости, проходящей через точку M (2;3;-4) параллельно плоскости yOz (перпендикулярно оси Ox ).

Так как yOz ||α, то уравнениеплоскости будет Ax+D =0. С другой стороны M Î α, поэтому 2A+D =0, D =-2A . Поэтому плоскость имеет уравнениеx -2=0.

Уравнение поверхности в пространстве

Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.

Общее уравнение плоскости

Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению:

Ax + By + Cz + D = 0,

где А, В, С - координаты вектора

вектор нормали к плоскости. Возможны следующие частные случаи:

А = 0 - плоскость параллельна оси Ох

В = 0 - плоскость параллельна оси Оу

С = 0 - плоскость параллельна оси Оz

D = 0 - плоскость проходит через начало координат

А = В = 0 - плоскость параллельна плоскости хОу

А = С = 0 - плоскость параллельна плоскости хОz

В = С = 0 - плоскость параллельна плоскости yOz

А = D = 0 - плоскость проходит через ось Ох

В = D = 0 - плоскость проходит через ось Оу

С = D = 0 - плоскость проходит через ось Oz

А = В = D = 0 - плоскость совпадает с плоскостью хОу

А = С = D = 0 - плоскость совпадает с плоскостью xOz

В = С = D = 0 - плоскость совпадает с плоскостью yOz

Уравнение плоскости, проходящей через три точки

Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой. Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат. Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М1, М2, М3 необходимо, чтобы векторы были компланарны.

Таким образом,

Уравнение плоскости, проходящей через три точки:

Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости

Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и вектор.

Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную точку М(х, у, z) параллельно вектору.

Векторы и вектор должны быть компланарны, т.е.

Уравнение плоскости:

Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости

Пусть заданы два вектора и, коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы должны быть компланарны. Уравнение плоскости:

Уравнение плоскости по точке и вектору нормали

Теорема. Если в пространстве задана точка М0(х0, у0, z0), то уравнение плоскости, проходящей через точку М0 перпендикулярно вектору нормали (A, B, C) имеет вид:

A(x - x0) + B(y - y0) + C(z - z0) = 0.

Доказательство. Для произвольной точки М(х, у, z), принадлежащей плоскости, составим вектор. Т.к. вектор - вектор нормали, то он перпендикулярен плоскости, а, следовательно, перпендикулярен и вектору. Тогда скалярное произведение

Таким образом, получаем уравнение плоскости

Теорема доказана.